2nBAT 2016 (4 punts)

Calculeu quantes solucions (x, y), amb x i y nombres enters positius, té l’equació 

x! · 7! = (x + y)!

A) Dues B) Una C) Cap D) Infinites E) Més de dues, però en nombre finit

ajuda i solució

1rESO 2020 (5 punts)

Diem que un nombre de tres xifres és bonic si la xifra central és més gran que la suma de les altres dues xifres. Quina és la quantitat més gran de nombres bonics consecutius que podem trobar?

A) 7   B) 6   C) 8   D) 9   E) 5 

ajuda i solució

2nESO 2020 (4 punts)

Si en Joan va a l’escola en bus i torna caminant, el viatge dura 30 minuts. Si va i torna en bus, el viatge dura 10 minuts. Quant de temps trigarà si va i torna caminant?

A) 50 minuts  B) 55 minuts  C) 40 minuts  D) 35 minuts  E) 45 minuts

ajuda i solució

3rESO 2020 (5 punts)

La Cinta té 52 triangles rectangles isòsceles idèntics. Vol construir un quadrat ajuntant alguns d’aquests triangles sense superposar-los. Quantes longituds diferents pot tenir el costat d’aquest quadrat?

A) 9   B) 3   C) 10   D) 5   E) 8

ajuda i solució

4tESO 2020 (5 punts)

1	12	7	14
8	13	2	10
11	3	16	5
15	6	9	4

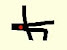
Hem fet servir els nombres de l’1 al 16 per a construir un quadrat màgic, però per error hem intercanviat dos dels nombres i hem obtingut el que es veu a la figura. Recordeu que, en un quadrat màgic, les sumes dels nombres de cada fila, de cada columna i de cada diagonal són totes iguals. Quina és la suma dels dos nombres intercanviats?

A) 21   B) 29   C) 13   D) 19   E) 15

ajuda i solució

1rBAT 2020 (5 punts)

Vuit nombres enters consecutius, positius i de tres xifres tenen la propietat següent: cadascun d’ells és divisible pel seu darrer dígit. Quina és la suma dels dígits del més petit dels vuit nombres enters? 

A) 12   B) 14   C) 13   D) 11   E) 10

ajuda i solució

2nBAT 2020 (4 punts)

Dels tres quadrats que es veuen en la figura, els dos més petits tenen àrees de 1 i 9. Quant val l’àrea del quadrat gran?

A) 100  B) 81  C) 80  D) 49  E) 82 

ajuda i solució

1rESO 2020 (5 punts)

En una gelateria, deu persones han fet els seus encàrrecs. Quatre han demanat gelat de vainilla; tres, de xocolata; dos, de llimona, i un, de mango. Els gelats van decorats, cada un amb un detall: quatre amb un paraigua, tres amb una cirera, dos amb una neula, i l’altre amb caramel. Tots els gelats que han encarregat són diferents.

Quina de les combinacions següents NO correspon a cap dels gelats que han pres?

A) Xocolata amb una cirera   B) Mango amb un paraigua   C) Vainilla amb caramel D) Llimona amb una neula   E) Vainilla amb un paraigua

ajuda i solució

2nESO 2020 (5 punts)

	Adam	Berta	Clara	David	Emili
Jutge I	2	0
Jutge II		2	0
Jutge III
Total	7	5	3	4	11

En un concurs cada un dels tres jutges (I, II i III) ha atorgat cinc puntuacions diferents: 0, 1, 2, 3 i 4 punts, una a cadascun dels cinc participants. A partir de les puntuacions individuals i totals que es veuen en la taula, deduïu quants punts ha donat el jutge III a l’Adam.

A) 3   B) 4   C) 1    D) 2    E) 0

ajuda i solució

 

3rESO 2020 (5 punts)

L’Anna, en Bernat i en Carles corren una cursa. Surten junts i cadascú manté una velocitat constant. Quan l’Anna arriba al final, a en Bernat li falten 15 m per a acabar, i a en Carles, 35m. Quan en Bernat acaba, a en Carles li queden 22 m. Quina és la longitud de la cursa?

A) 140m B) 150m C) 175m D) 135m E) 165m

ajuda i solució

4tESO 2020 (5 punts)

 

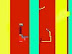
Tres pirates i tres dracs estan asseguts en una taula rodona. Els dracs diuen sempre la veritat i els pirates menteixen sempre, o potser és a l’inrevés, no ho sabem. Se sap que un dels sis va robar una moneda i a tots sis se’ls fa la pregunta: “Està assegut al teu costat qui va robar la moneda?”. Les seves respostes i la manera com estaven asseguts es veuen en la imatge. Qui va robar la moneda?

A) EldracA   B) EldracB   C) ElpirataC   D) El pirataD   E) El dracE

ajuda i solució

!rBAT 2020 (5 punts)

1		6	3
	2	2	8
	7		4
X		7

En cadascun dels quadrats s’ha d’escriure un nombre de manera que la suma dels quatre nombres de cada fila i de cada columna sigui la mateixa. Quin nombre va al quadrat amb una X?

A) 6    B) 9    C) 8    D) 5    E) 7

ajuda i solució

2nBAT 2016 (4 punts)

Tenim nou nombres ordenats en ordre ascendent. El nombre del mig és, també, la mitjana aritmètica dels nou nombres. La mitjana aritmètica dels cinc més grans és 68 i la dels cinc més petits, 44. Quant fa la suma dels nou nombres?

A) 560   B) 514   C) 504   D) 112   E) 56

ajuda i solució

UN PROBLEMA DEL SEGLE PASSAT

Un trapezi ABCD té costats paral·lels de longitud AB=40cm i CD=16cm. El punt P està sobre AB de manera que el segment DP divideix el trapezi en dues parts de la mateixa àrea. Calculeu la longitud de AP expressada en centímetres.

A) 16  B) 20   C) 28   D) 32   E) 36

ajuda i solució

UN SENZILL PROBLEMA DE LÒGICA

En Marc agafa tres cartes d’un joc amb set cartes numerades de l’1 al 7, en Joan n’agafa dues i queden dues cartes a taula. En Marc mira només les seves cartes i diu a en Joan:”Sé que les teves cartes sumen un nombre parell”. Quant sumen les cartes d’en Marc?

A) 10   B) 15   C) 6   D) 9   E) 12

ajuda i solució

 

2nBAT 2016 (5 punts)

Un robot es troba a l’origen del pla cartesià. Llancem alhora dos daus, un vermell i un blau. Si el nombre del dau vermell és parell, el robot avanc ̧a una unitat cap a la dreta, i si és senar, cap a l’esquerra. Si el nombre del dau blau és parell, el robot avança una unitat cap amunt, i si és senar, cap avall. Quina és la probabilitat que el robot torne a l’origen després de llançar dues vegades els dos daus?

A) 1/2   B) 1/3   C) 1/9   D) 1/6   E) 1/4

ajuda i solució

 

1rBUP 2016 (5 punts)

Si f és una funció real de variable real que compleix:

f (2x + 1) = 4x² + 14x 

per a tots els nombres reals x, quina és la suma de les solucions reals de l’equació f (x) = 0?

A) -6   B) -5   C) 0   D) 5   E) 6

ajuda i solució

4tESO 2016 (5 punts)

Si U+V=1 i U²+V²=2, quant és U⁴+V⁴ ?

A) 4    B) 8    C) 1    D) 3    E) 3’5

ajuda i solució

3rESO 2016 (4 punts)

2016 habitants viuen en el mateix poble. Cap d’ells no té més de 49 anys. Quants habitants podem assegurar que tenen la mateixa edat? 

A) Al menys 39, però a priori no podem dir que siguen 40 o més. 

B) Al menys 40, però a priori no podem dir que siguen 41 o més.

C) Al menys 41, però a priori no podem dir que siguen 42 o més.

D) Al menys 42, però a priori no podem dir que siguen 43 o més.

E) Al menys 43, però a priori no podem dir que siguen 44 o més.

ajuda i solució